Círculo trigonométrico y funciones trigonométricas

¿Qué es el círculo trigonométrico y funciones trigonométricas?

 Es un círculo unitario que tiene su centro en el origen de coordenadas y su radio mide la unidad. Es una herramienta que se utiliza en conceptos de trigonometría y además nos ayuda a fundamentar las funciones trigonométricas.

Con el círculo trigonométrico podemos obtener el valor de las razones trigonométricas para cierto ángulo, además también se puede utilizar para obtener las identidades pitagóricas.

Para obtener las funciones trigonométricas se toma como base un círculo de radio 1 con centro en el origen, se toma un ángulo medido a partir del eje x positivo y en sentido contrario de las manecillas del reloj.

Círculo trigonométrico y funciones trigonométricas

Seno de α

Partiendo del ángulo α y la recta r se obtiene un punto P, si se traza una línea perpendicular desde ese punto y hacia el eje Y se obtiene un segmento OB que se denomina seno de α.

Coseno de α

Partiendo del ángulo α y la recta r se obtiene un punto P, si se traza una línea perpendicular desde ese punto y hacia el eje X se obtiene un segmento OA que se denomina coseno de α.

Tangente de α

Una línea tangente es la que solo toca en un punto a la circunferencia.

Cotangente de α

Si trazamos una recta FD que sea tangente al punto F y que toque a la recta OD, FD es cotangente de α.

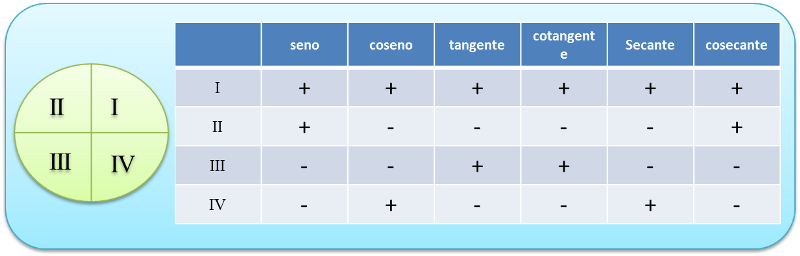
Cuadrantes del círculo trigonométrico

Si dividimos el círculo en 4 partes iguales a cada parte se le conoce como cuadrante, en cada cuadrante las funciones seno, coseno , tangente y cotangente cambian su valor.

Primer cuadrante

Si aumenta el ángulo α disminuye el valor del coseno y  de la cotangente pero aumenta el valor de la tangente y del seno.

Segundo cuadrante

Si aumenta el ángulo α, disminuye el valor del seno, del coseno, de la tangente y de la cotangente.

Tercer cuadrante

Si aumenta el ángulo α, disminuye el valor del seno, del coseno y de la cotangente pero aumenta el valor de la tangente.

Cuarto cuadrante

Si aumenta el ángulo α, disminuye el valor del seno y de la tangente pero aumenta el valor del coseno y de la cotangente.